Many-body physics in spinor Bose-Einstein condensates
Introduction
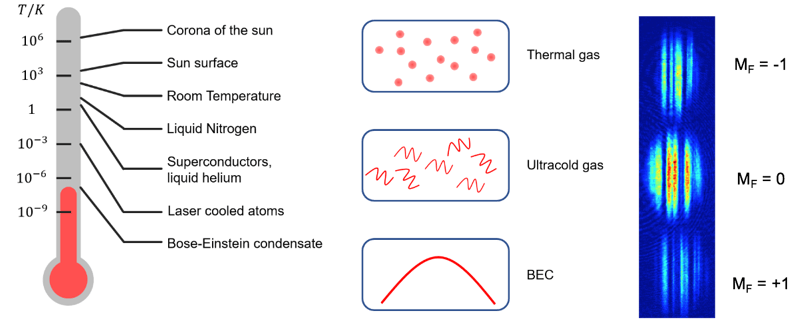
At different temperatures, matter displays different states. Bose-Einstein condensate (BEC) is a state of matter where the particles (bosons) are cooled to nearly the absolute zero (<microkelvin) and form a collective quantum wave. As predicted by quantum mechanics, its emergence comes from the overlapping of matter waves when the temperature goes down. Spinor BECs, as our main research focus, arise when the bosons have internal hyperfine structures. They offer a rich arena for the exploration of many-body physics since both the spin and spatial degrees of freedom play a role in the description of a quantum state.
Quantum phase transition in spinor BECs
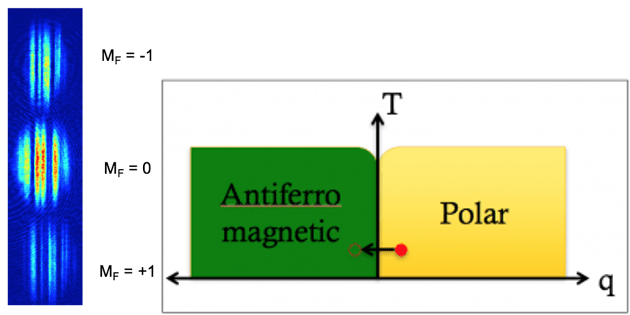
Spinor Bose-Einstein condensates (BECs) are quantum gases where the hyperfine spin F is a free variable. They offer a rich arena for the exploration of many-body physics since both the spin and spatial degrees of freedom play a role in the description of a quantum state. An interplay between internal and external interactions leads to novel quantum phases and domains of different spin orientations. The image on the left shows a spin-1 BEC that has spontaneously formed spin structures with a fluctuating local value of the spin projection M_F. Such structures are formed by quenching the condensate from the polar phase to the antiferromagnetic phase. The cloud of atoms was subject to time-of-flight Stern-Gerlach separation of the three spin components before imaging.
Links to publications
Quantum Phase Transition in an Antiferromagnetic Spinor Bose-Einstein Condensate
Antiferromagnetic Spatial Ordering in a Quenched One-dimensional Spinor Gas
Solitary excitations in spinor BECs
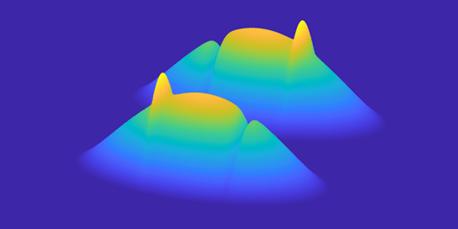
We are currently focused on studying the magnetic solitons in antiferromagnetic spin-1 BECs. As stable and localized excitations in nonlinear systems, solitons play an important role in many fields of physics, ranging from cosmology to fiber optics. Recently we exploited the phase imprinting method and successfully generated a pair of magnetic solitons in a spin-1 BEC, where each of the soliton consists of a density bump in the M_F=+1 (-1) component and a density notch in the M_F=-1 (+1) component. The figure on the left shows the propagation of a pair of magnetic solitons on top of a balanced mixture of M_F=+-1 condensates.
Links to publications
Magnetic Solitons in a Spin-1 Bose-Einstein Condensate
Magnetic soliton: from two to three components with SO(3) symmetry
Magnetic solitons in an immiscible two-component Bose-Einstein condensate